复杂网络仿真入门到精通5-网络动力学

系列文章：

• 系列合集

• 本文为《复杂网络仿真入门到精通》系列第5篇。
  前几篇主要介绍了网络的结构特征，这一篇我们将正式进入网络动力学领域——让网络“动”起来。

系列文章：

• 系列合集
• 下一篇预告：网络鲁棒性分析

本文对应资源：
github代码地址：复杂网络学习合集-step5
如访问不了可从下列地址保存：第一个文件夹 下面的 Step5
网盘地址

一、什么是网络动力学？

网络动力学研究的是：

在一个由节点和边组成的系统中，状态如何随时间演化。

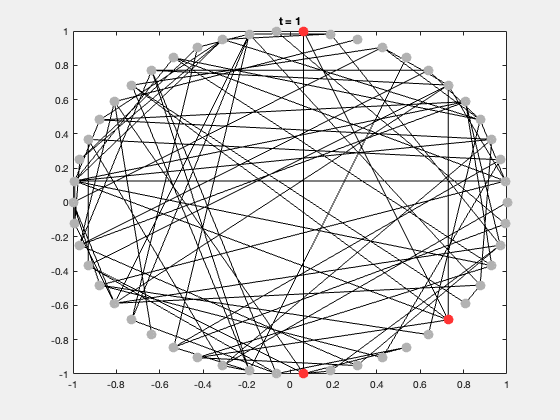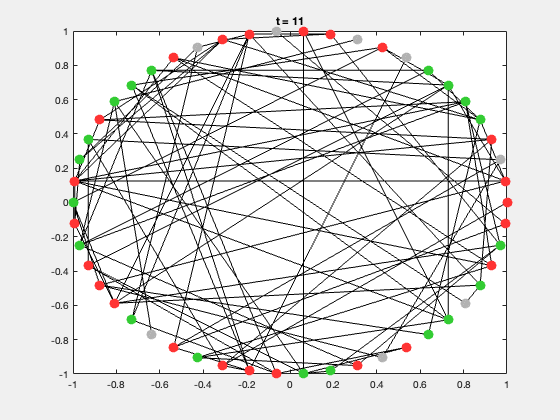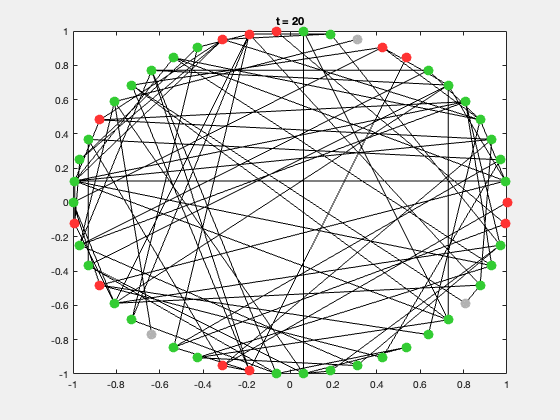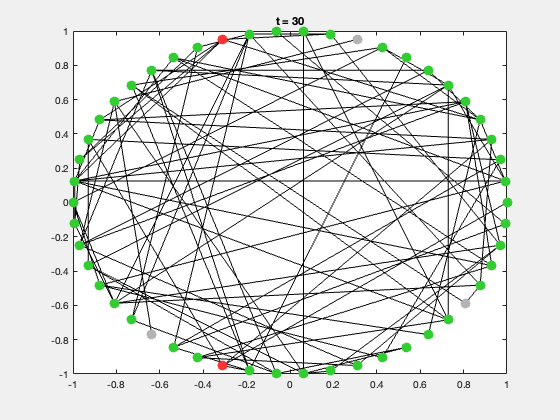
典型的研究问题包括：

• 传染病在社交网络中的传播；
• 信息在社交平台上的扩散；
• 电力网络或神经网络的同步；
• 系统中失效的传播。

抽象公式：
$$
x_i(t+1) = f(x_i(t), {x_j(t)}_{j \in N_i})
$$

其中：

• $x_i(t)$：节点 $i$ 在时刻 $t$ 的状态；
• $N_i$：与节点 $i$ 相连的邻居集合；
• $f(\cdot)$：状态更新规则。

---

二、SIR 传染病模型概述

SIR 模型是网络动力学中最经典的传播模型。
每个节点有三种状态：

状态	含义	颜色
S	易感者（Susceptible）	灰色
I	感染者（Infected）	红色
R	康复者（Recovered）	绿色

状态转移规则：
$$
S + I \xrightarrow{\beta} 2I, \quad I \xrightarrow{\gamma} R
$$

• 感染率 $\beta$：感染者以概率传播给邻居
• 康复率 $\gamma$：感染者以概率康复

三、Python 实现

下面是一个简单可复现的 Python 版本，用于模拟传播过程：

import networkx as nx
import random
import matplotlib.pyplot as plt

# 构建网络
G = nx.erdos_renyi_graph(50, 0.05)

# 初始化节点状态
state = {node: 'S' for node in G.nodes()}
state[random.choice(list(G.nodes()))] = 'I'

beta = 0.3
gamma = 0.1
steps = 30

# 仿真
for t in range(steps):
    new_state = state.copy()
    for node in G.nodes():
        if state[node] == 'I':
            for nbr in G.neighbors(node):
                if state[nbr] == 'S' and random.random() < beta:
                    new_state[nbr] = 'I'
            if random.random() < gamma:
                new_state[node] = 'R'
    state = new_state.copy()

    # 绘图
    color_map = {'S': 'skyblue', 'I': 'red', 'R': 'gray'}
    colors = [color_map[state[n]] for n in G.nodes()]
    nx.draw(G, node_color=colors, with_labels=False)
    plt.title(f'Time step {t}')
    plt.pause(0.3)
    plt.clf()

四、MATLAB 实现（直接输出仿真图）

MATLAB 版本可以直接显示传播过程的静态图或逐步演示：

%% 复杂网络 SIR 模型仿真（MATLAB 可视化示例）
clc; clear; close all;

%% 网络参数
N = 50;           % 节点数
p = 0.07;         % ER 网络连边概率
steps = 30;       % 仿真步数

%% 构建随机网络（ER 网络）
G = rand(N) < p;
G = triu(G,1);    % 只保留上三角
G = G + G';       % 对称邻接矩阵

%% 初始化节点状态
state = repmat("S", N, 1); % 全部初始为易感者
state(randi(N)) = "I";     % 随机选择一个感染者

%% SIR 模型参数
beta = 0.3;   % 感染率
gamma = 0.1;  % 康复率

%% 节点布局（圆形）
theta = linspace(0, 2*pi, N+1);
pos = [cos(theta(1:N))', sin(theta(1:N))'];

%% 定义颜色映射
color_map = containers.Map(["S","I","R"], ...
                          {[0.7 0.7 0.7], ...  % S 灰色
                           [1 0.2 0.2], ...    % I 红色
                           [0.2 0.8 0.2]});    % R 绿色

%% 仿真循环
figure('Position',[100 100 600 600]);
for t = 1:steps
    new_state = state;
    
    % 状态更新
    for i = 1:N
        if state(i) == "I"
            neighbors = find(G(i,:));
            for j = neighbors
                if state(j) == "S" && rand < beta
                    new_state(j) = "I";
                end
            end
            if rand < gamma
                new_state(i) = "R";
            end
        end
    end
    state = new_state;
    
    % 绘制网络
    clf;
    gplot(G, pos, 'k-');  % 绘制连边
    hold on;
    
    % 每个节点的颜色
    node_colors = zeros(N,3);
    for k = 1:N
        node_colors(k,:) = color_map(state(k));
    end
    
    scatter(pos(:,1), pos(:,2), 100, node_colors, 'filled');
    title(['SIR 网络仿真, t = ' num2str(t)]);
    axis equal;
    axis off;
    drawnow;
end

每次运行都会生成一个动态展示，节点颜色随状态变化，可直观展示传播过程。

---

五、总结与延伸

• 网络动力学让静态网络“动”起来，能够模拟现实中各种传播过程。

• Python 适合逻辑演示与快速实验，MATLAB 适合可视化展示。

• 后续可拓展：

  • 不同网络拓扑（无标度、小世界、随机网络）下的传播比较
  • SI、SIS、SEIR 等模型
  • 异质节点参数或动态网络演化

---

下一节预告

《复杂网络仿真入门到精通6：鲁棒性分析》
学习网络在攻击或故障下的稳定性。