复杂网络仿真入门到精通4: 社团结构分析

Posted on October 22, 2025 本文总阅读量加载中... 次

系列文章：

系列合集

下一篇预告：网络鲁棒性分析

一、引言：社团结构的重要性

社团结构（Community Structure）是复杂网络研究中最具代表性的现象之一。
它描述了网络中节点之间形成紧密连接群体的现象，在社交网络、科研合作网络、生物网络中普遍存在。

社交网络：社团对应朋友圈或兴趣群体；
科研合作网络：社团对应研究方向或课题组；
生物网络：社团对应功能模块（如基因调控模块）。

通过社团分析，我们可以理解网络的宏观组织形态、发现潜在的功能群体，并进一步优化传播、推荐或控制机制。
因此，社团检测已成为复杂网络分析中最核心的研究内容之一。

本文对应资源：
github代码地址：复杂网络学习合集-step4
如访问不了可从下列地址保存：第一个文件夹下面的 Step4
网盘地址

二、社团检测的基本思路

社团划分的目标是：

让社团内部的连接尽量密集，而社团之间的连接尽量稀疏。

目前主流方法大致可以分为三类：

方法类别	主要思想	常用算法
基于模块度优化（Modularity）	通过最大化模块度 (Q) 寻找最优划分	Louvain、Newman
基于谱聚类（Spectral）	对网络拉普拉斯矩阵进行特征分解	Spectral Clustering
基于概率模型	用随机块模型（SBM）建模节点连接概率	Stochastic Block Model

这些方法各有优势：

Louvain 方法高效、适用于大规模网络；
谱聚类方法理论清晰、便于可解释；
概率模型适合推断复杂多层网络。

三、MATLAB 实现：Louvain 社团检测

在 MATLAB 中，我们通常先构建网络（或载入上一节课程保存的邻接矩阵），然后执行社团检测。
最常见的是 Louvain 算法，它通过模块度 (Q) 的优化自动识别社团。

关键示例：

1
2
3

G = graph(A);
[community, Q] = community_louvain(full(adjacency(G)));
fprintf('模块度 Q = %.4f\n', Q);

得到的结果中：

community 表示每个节点所属社团编号；
Q 为模块度值，衡量社团划分质量。

随后可使用 force-directed 布局进行可视化：

p = plot(G, 'Layout', 'force');
colors = lines(max(community));
for i = 1:max(community)
    highlight(p, find(community==i), 'NodeColor', colors(i,:));
end

若模块度 (Q > 0.3)，说明网络具有明显的社团结构。

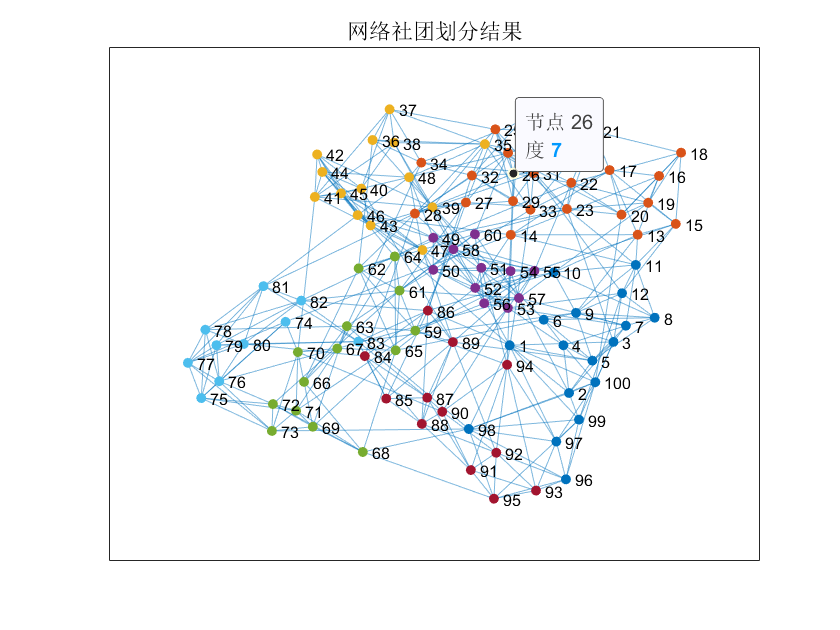
四、模块度与网络类型的关系

模块度 ( Q ) 的定义为：

$$Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j)$$

其中：

$(A_{ij})$：邻接矩阵；
$(k_i)$：节点 $(i)$ 的度；
$(m)$：边总数；
$(\delta(c_i, c_j))$：若节点 $(i,j) $属于同一社团则为 1，否则为 0。

根据经验：

(Q > 0.3)：网络具有显著社团结构；
(Q < 0.1)：社团结构不明显。

结合前几篇结果，我们可以对网络类型进行对比：

网络类型	主要特征
小世界网络	高聚类系数 + 短平均路径
无标度网络	度分布呈幂律
社团网络	模块度 (Q) 高，结构分层明显

这三类特性经常同时出现在现实系统中，例如社交网络既呈幂律分布，又具有小世界和社团特性。

五、社团结构的功能与桥节点分析

完成社团划分后，我们往往还需识别社团间的关键节点。
这些节点在不同社团间起“桥梁作用”，对信息传播或控制极为关键。

在 MATLAB 中，可以使用介数中心性（Betweenness Centrality）来识别桥节点：

1
2
3

bet = centrality(G, 'betweenness');
[~, idx] = max(bet);
fprintf('桥节点编号：%d\n', idx);

随后进行可视化：

1 2	highlight(p, idx, 'NodeColor', 'k', 'Marker', 's', 'MarkerSize', 8); title('桥节点高亮');

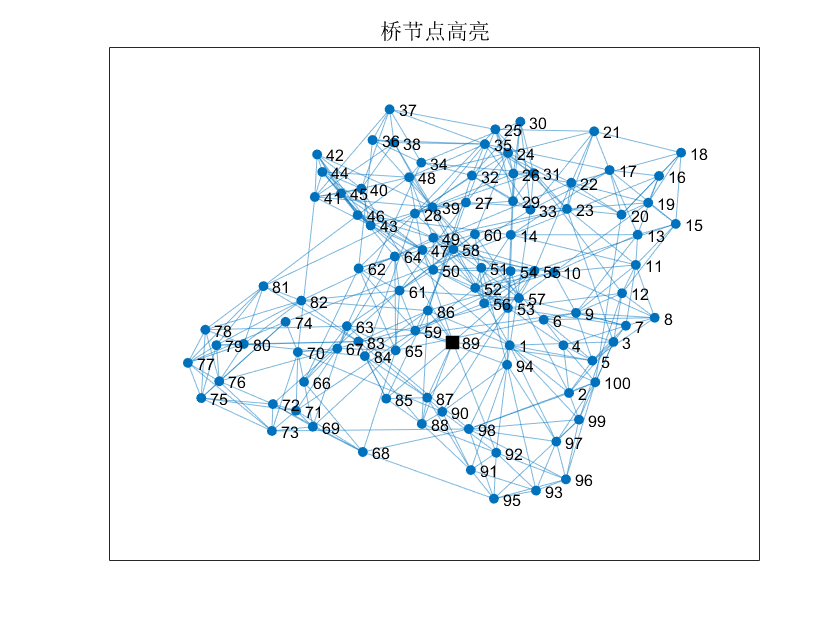
此外，还可以分析不同社团间的连接强度：

1
2
3

imagesc(commMatrix);
colorbar;
title('社团间连接强度矩阵');

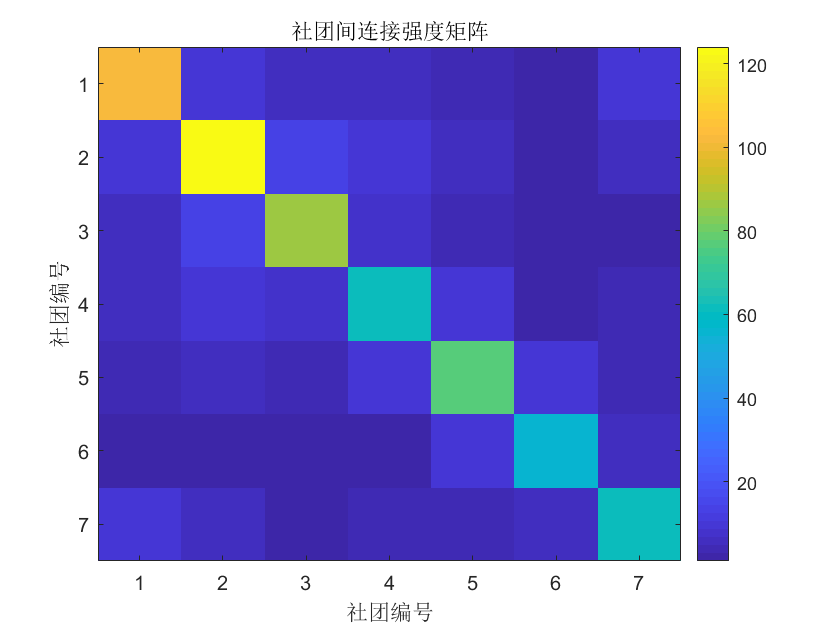
从矩阵图中，我们能清晰看到哪些社团之间的交互更频繁。

六、科研视角的延伸与应用

社团检测不仅是可视化的结果，更是理解复杂系统组织规律的关键工具。
在科研与工程应用中，常见的拓展方向包括：

社团动态演化
研究社团随时间变化的形成与合并过程，例如社交话题的生命周期。
多层网络社团检测
当网络存在多种关系（如“合作”与“引用”），需要分析不同层的社团重叠与耦合。
基于社团的功能预测
通过节点所属社团，预测其潜在属性或未来连接。

推荐阅读：

Newman, M. E. J. Networks: An Introduction. Oxford University Press, 2010.
Fortunato, S. Community Detection in Graphs. Physics Reports, 2010.

七、小结与下一步

本节我们完成了：

✅ 理解社团结构的概念与意义；
✅ 掌握 Louvain 算法的基本实现；
✅ 通过模块度分析网络结构特性；
✅ 识别关键桥节点并可视化社团分布。

最后：给大家推荐一个在线复杂计算平台, 欢迎大家进行体验

👉 复杂网络分析平台

支持：

AI 智能报告生成
上传邻接矩阵文件；
自动构建网络, 指标一键计算与可视化；
网络鲁棒性分析（节点/边攻击）
级联失效模型分析