复杂网络仿真入门到精通8:网络鲁棒性理论基础
双十一福利|复杂网络仿真平台送 6 次计算 + 七折优惠 🎁
最近在做实验的人是不是都有这种感觉:仿真老是跑不动,代码环境还容易出错……
这次终于有点小福利可以薅一下羊毛了 😎
复杂网络仿真平台 搞了个 双十一活动:
所有注册用户都能直接领 6 次专业版仿真次数,
不需要抽奖,不需要转发,登录就有!
并且活动期间还享有:
✨ 七折优惠 + 额外赠送 15 次专业计算额度!
🧠 它能干嘛?
其实平台挺方便的,主要是给做复杂网络方向的人用的:
- 直接上传 邻接矩阵、CSV 数据
- 自动计算各种 网络指标、社团划分、鲁棒性分析、级联失效模型分析
- 支持在线可视化绘图与结果导出
- 最关键是:不用安装环境,打开网页就能跑!
对写论文、课程设计、科研项目都很实用。
我自己跑过几次,基本 一分钟出结果 ⚡。
📅 活动时间
🗓️ 11 月 10 日 — 11 月 18 日
期间注册或者登录账号就能看到次数已经到账。
如果用着不错,还能在反馈里多拿几次赠送次数。
🔗 平台入口
👉 复杂网络仿真平台
💻 建议使用 电脑端 打开,体验更顺畅。
💬 想法与反馈
平台其实是我自己开发的,想让复杂网络分析更简单点,别被一堆依赖卡死。
有啥建议或者想法可以直接找我聊~
我平时也在用,
能帮你看看数据怎么跑更快、模型怎么设置更合适。
希望这次双十一活动能帮你省点时间,也跑出更漂亮的图! 🕸️
在Java中调用MATLAB函数的完整流程:从打包 jar 到服务器部署
为什么在 Java 中调用 MATLAB 函数?
最近在做复杂网络仿真平台时,需要在 Java 环境中调用一些 MATLAB 编写的算法函数。这些函数在matlab中已经调试好经过了验证,就不想在java换再实现一套同样的逻辑。
一开始以为会很麻烦,后来发现 MATLAB 官方其实提供了完整的 Java 支持。其实就是用 MATLAB Compiler SDK 就能直接导出 .jar 文件,然后在 Java 项目中调用。然后配置好环境就可以轻松运行了。
这篇文章记录完整流程:
- MATLAB 如何导出 jar
- 本地如何配置运行环境
- 服务器端如何部署(含 MATLAB Runtime)
一、MATLAB 导出 jar 包
MATLAB 自带 Compiler SDK,可以把 .m 文件打包成 Java 可调用的 jar。
示例函数:
1 | % add.m |
然后在当前函数(add.m)文件下 在 MATLAB 的命令行执行:
1 | mcc -W 'java:addClass,AddClass' -T link:lib add.m |
执行后会生成:
AddClass.jarAddClass.ctf- 以及
for_testing文件夹等辅助内容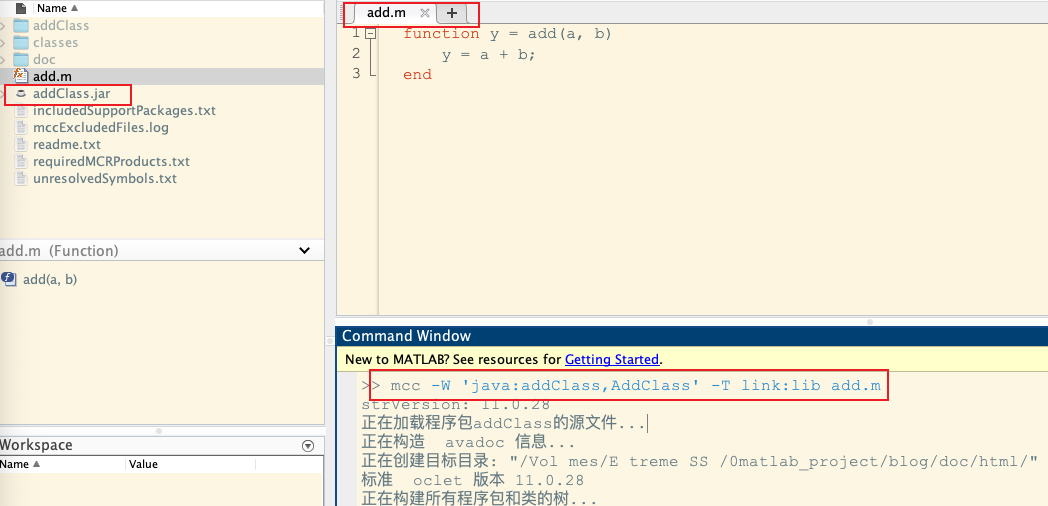
二、本地环境配置(Java 调用)
在本地 Java 项目中使用刚生成的 jar。
假设使用 IntelliJ IDEA。
1. 导入文件
将 AddClass.jar、AddClass.ctf 放到工程文件夹下的 libs/ 文件夹。
2. 添加依赖
添加 MATLAB runtime 依赖 javabuilder.jar:
示例位置
1 | C:\Program Files\MATLAB\R2023a\toolbox\javabuilder\jar\javabuilder.jar |
Maven:根据你的项目结构和具体javabuilder.jar位置,添加如下依赖
1 | <dependency> |
Gradle:
根据你的项目结构和具体javabuilder.jar位置,添加如下依赖:
1 | dependencies { |
3. Java 调用代码
1 | import addClass.AddClass; |
4. 环境变量
MATLAB Runtime (MCR) 必需。
若未安装 MATLAB,则需单独安装对应版本。
下载地址:
https://www.mathworks.com/products/compiler/matlab-runtime.html
然后配置路径
1 | set PATH=%PATH%;C:\Program Files\MATLAB\MATLAB Runtime\v910\runtime\win64 |
三、服务器部署(Linux 环境)
1. 安装 MATLAB Runtime
下载地址:
https://www.mathworks.com/products/compiler/matlab-runtime.html
选择与打包版本匹配的 runtime版本,例如 R2023a → v910。
安装路径示例:/usr/local/MATLAB/MATLAB_Runtime/v910/
2. 配置环境变量
编辑 /etc/profile:
1 | export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/MATLAB/MATLAB_Runtime/v910/runtime/glnxa64 |
执行 source /etc/profile。
3. 运行 Java 程序
1 | java -cp .:AddClass.jar:/usr/local/MATLAB/MATLAB_Runtime/v910/java/jar/javabuilder.jar TestMatlab |
输出:
1 | Result = 3.0 |
我当时是使用docker构建镜像的,遇到了好几个问题,最后Dockerfile 部分内容如下:
1 | # ------------------------------ |
四、常见问题
| 问题 | 原因 | 解决办法 |
|---|---|---|
| java.lang.UnsatisfiedLinkError | Runtime 库未配置 | 检查 LD_LIBRARY_PATH |
| Could not find library mclmcrrt9_10.dll | MCR 未安装或版本不匹配 | 安装对应版本 MCR |
| ClassNotFoundException | jar 路径错误 | 检查 classpath |
| 输出为空或异常退出 | CTF 路径错误 | 保证 .ctf 文件与 jar 同目录 |
五、总结
虽然也是踩坑了,不过整个过程其实不复杂:
- MATLAB 打包 jar
- Java 添加依赖
- 安装并配置 Runtime
- 成功运行
如果部署在服务器上,建议把 MATLAB 模块单独封装成服务(如 Flask / SpringBoot 接口),通过 HTTP 调用,这样更容易维护和扩展。
感谢大家的观看,希望这篇文章能帮到有类似需求的朋友!
复杂网络仿真入门到精通5-网络动力学
系列文章:
- 本文为《复杂网络仿真入门到精通》系列第5篇。
前几篇主要介绍了网络的结构特征,这一篇我们将正式进入网络动力学领域——让网络“动”起来。
系列文章:
- 系列合集
- 下一篇预告:网络鲁棒性分析
本文对应资源:
github代码地址:复杂网络学习合集-step5
如访问不了可从下列地址保存:第一个文件夹 下面的 Step5
网盘地址
一、什么是网络动力学?
网络动力学研究的是:
在一个由节点和边组成的系统中,状态如何随时间演化。
典型的研究问题包括:
- 传染病在社交网络中的传播;
- 信息在社交平台上的扩散;
- 电力网络或神经网络的同步;
- 系统中失效的传播。
抽象公式:
$$
x_i(t+1) = f(x_i(t), {x_j(t)}_{j \in N_i})
$$
其中:
- $x_i(t)$:节点 $i$ 在时刻 $t$ 的状态;
- $N_i$:与节点 $i$ 相连的邻居集合;
- $f(\cdot)$:状态更新规则。
二、SIR 传染病模型概述
SIR 模型是网络动力学中最经典的传播模型。
每个节点有三种状态:
| 状态 | 含义 | 颜色 |
|---|---|---|
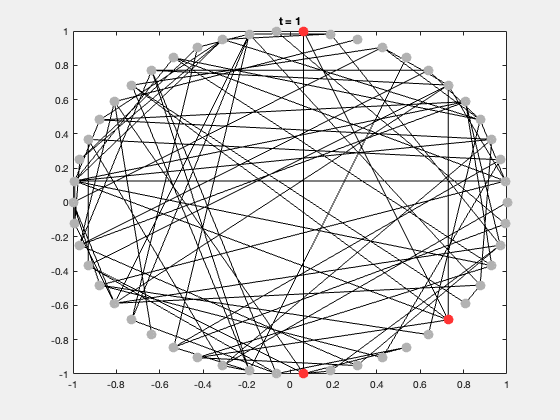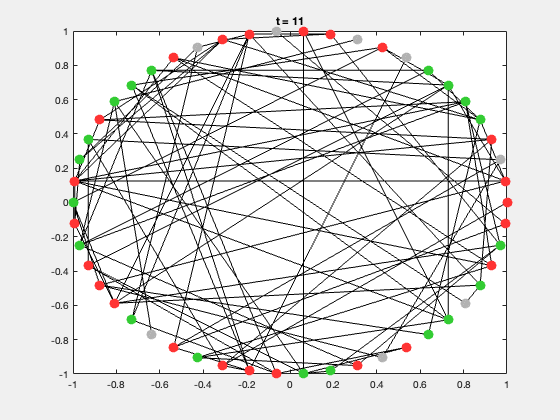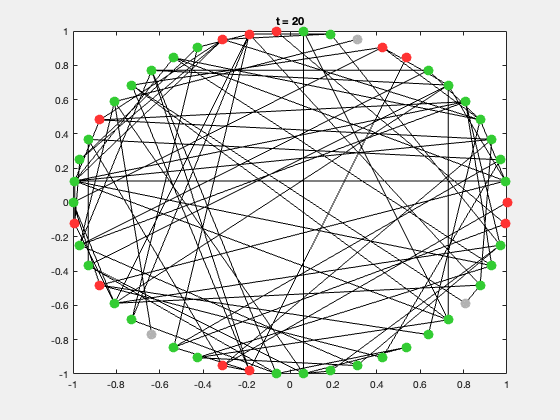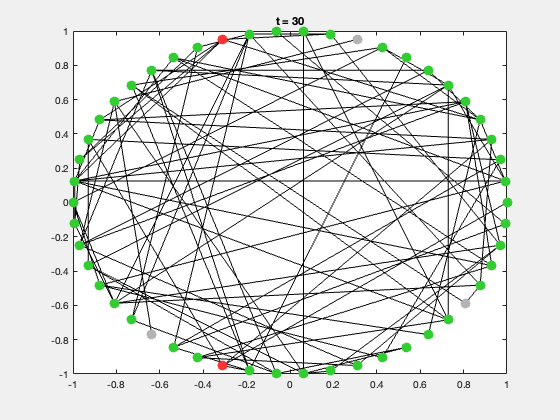
| S | 易感者(Susceptible) | 灰色 |
| I | 感染者(Infected) | 红色 |
| R | 康复者(Recovered) | 绿色 |
状态转移规则:
$$
S + I \xrightarrow{\beta} 2I, \quad I \xrightarrow{\gamma} R
$$
- 感染率 $\beta$:感染者以概率传播给邻居
- 康复率 $\gamma$:感染者以概率康复
三、Python 实现
下面是一个简单可复现的 Python 版本,用于模拟传播过程:
1 | import networkx as nx |
四、MATLAB 实现(直接输出仿真图)
MATLAB 版本可以直接显示传播过程的静态图或逐步演示:
1 | %% 复杂网络 SIR 模型仿真(MATLAB 可视化示例) |
每次运行都会生成一个动态展示,节点颜色随状态变化,可直观展示传播过程。
五、总结与延伸
网络动力学让静态网络“动”起来,能够模拟现实中各种传播过程。
Python 适合逻辑演示与快速实验,MATLAB 适合可视化展示。
后续可拓展:
- 不同网络拓扑(无标度、小世界、随机网络)下的传播比较
- SI、SIS、SEIR 等模型
- 异质节点参数或动态网络演化
下一节预告
《复杂网络仿真入门到精通6:鲁棒性分析》
学习网络在攻击或故障下的稳定性。
复杂网络学习资源整理(持续更新)
本文整理了复杂网络(Complex Networks)学习与研究的常用资源,包括教材、论文、算法、数据集、工具和开源代码库,帮助你从入门到实战快速建立体系。
一、📘 入门书籍与经典教材
| 书名 | 作者 | 简介 |
|---|---|---|
| Networks: An Introduction | Mark Newman | 最经典的复杂网络教材,系统讲解理论、指标与模型。 |
| Graph Theory and Complex Networks | Maarten van Steen | 免费英文教材(可在线获取),兼顾图论与网络科学。 |
| 复杂网络理论及其应用 | Albert-László Barabási | 很好的中文教材。 |
注:我已经整理好对应资源,文末网盘链接自取
二、📄 经典论文与里程碑成果
| 主题 | 论文 | 出版 |
|---|---|---|
| 小世界网络 | Watts & Strogatz, Nature, 1998 | 提出小世界模型,揭示真实网络的高聚类与短路径特征。 |
| 无标度网络 | Barabási & Albert, Science, 1999 | 提出幂律分布模型,奠定复杂网络理论基础。 |
| 社区发现综述 | Newman, SIAM Review, 2003 | 系统总结了网络划分与社区检测方法。 |
| 网络鲁棒性 | Albert et al., Nature, 2000 | 分析复杂网络在攻击下的连通性与失效特性。 |
三、🧠 核心概念与常用算法
网络结构指标
- 度分布(Degree Distribution)
- 平均路径长度(Average Path Length)
- 聚类系数(Clustering Coefficient)
- 网络密度与连通性
社区发现算法
- Louvain 算法(模块度最大化)
- Label Propagation(标签传播)
- Girvan–Newman(基于介数中心性)
中心性指标
- 度中心性、介数中心性、接近中心性
- 特征向量中心性、PageRank
网络动力学模型
- 传播模型:SIR、SIS、Rumor Model
- 级联失效模型:负载重分配、鲁棒性分析
- 演化模型:BA、WS、ER 随机网络生成
四、💻 常用开源库与工具
Python
- NetworkX — 功能最全的复杂网络库
- igraph (Python版) — 高性能计算,支持大规模图
Java
- JGraphT — 功能丰富的图算法库(最短路径、连通性、流计算)
R
- igraph (R版) — 与 Python 版类似,科研论文常用
- statnet / sna — 专注社会网络分析
五、📊 网络数据集资源
| 名称 | 链接 | 简介 |
|---|---|---|
| KONECT | https://konect.cc/ | 大规模网络数据集集合,包含社交、通信、生物网络等。 |
| SNAP (Stanford) | https://snap.stanford.edu/data/ | 斯坦福网络分析平台,提供学术常用图数据。 |
| Network Repository | https://networkrepository.com/ | 在线浏览和下载多种类型的网络数据。 |
| ICON Dataset | https://icon.colorado.edu/ | 社会与行为网络数据集。 |
六、🖥️ 可视化与分析工具
| 工具 | 特点 |
|---|---|
| Gephi | 桌面可视化分析工具,支持社区检测、布局算法、交互分析。 |
| Cytoscape | 生物信息学常用,可扩展插件丰富。 |
| Graphia | 轻量可视化与聚类分析工具。 |
| D3.js | Web 端可视化,适合前端展示与交互开发。 |
七、🌐 在线平台与实战项目
- 复杂网络计算平台 — 在线级联失效模拟、鲁棒性分析、网络指标计算与可视化平台。
- NetworkX Documentation — 官方教程与示例。
八、🎯 我总结的资源
1. 📂 代码仓库
- complex-network-study —— 复杂网路学习路线
2. 📘 教程与学习笔记
- 复杂网络仿真入门到精通(系列) —— 详细解析 复杂网络的仿真内容,。
- B站视频教程:复杂网络仿真入门到精通
3. 📝 博客与资料整理
4. 🔗 个人平台与工具网站
复杂网络计算平台 — 在线级联失效模拟、鲁棒性分析、网络指标计算与可视化平台。
支持邻接矩阵上传、网络可视化、网络鲁棒性分析、级联失效模拟与指标计算。
5. 🔗 网盘资源
- 资源合集
包含书籍、论文、代码与数据集等,持续更新中。
💬 结语
复杂网络作为跨学科研究的重要方向,已经在社会学、生物学、计算机科学等领域广泛应用。
希望这份资源整理能帮助你快速建立知识体系,找到适合自己的研究或开发方向。
📌 持续更新中,欢迎收藏或补充。
如果你有推荐资源或开源项目,欢迎留言交流!
复杂网络仿真入门到精通4: 社团结构分析
系列文章:
- 系列合集
- 下一篇预告:网络鲁棒性分析
一、引言:社团结构的重要性
社团结构(Community Structure)是复杂网络研究中最具代表性的现象之一。
它描述了网络中节点之间形成紧密连接群体的现象,在社交网络、科研合作网络、生物网络中普遍存在。
- 社交网络:社团对应朋友圈或兴趣群体;
- 科研合作网络:社团对应研究方向或课题组;
- 生物网络:社团对应功能模块(如基因调控模块)。
通过社团分析,我们可以理解网络的宏观组织形态、发现潜在的功能群体,并进一步优化传播、推荐或控制机制。
因此,社团检测已成为复杂网络分析中最核心的研究内容之一。
本文对应资源:
github代码地址:复杂网络学习合集-step4
如访问不了可从下列地址保存:第一个文件夹 下面的 Step4
网盘地址
二、社团检测的基本思路
社团划分的目标是:
让社团内部的连接尽量密集,而社团之间的连接尽量稀疏。
目前主流方法大致可以分为三类:
| 方法类别 | 主要思想 | 常用算法 |
|---|---|---|
| 基于模块度优化(Modularity) | 通过最大化模块度 (Q) 寻找最优划分 | Louvain、Newman |
| 基于谱聚类(Spectral) | 对网络拉普拉斯矩阵进行特征分解 | Spectral Clustering |
| 基于概率模型 | 用随机块模型(SBM)建模节点连接概率 | Stochastic Block Model |
这些方法各有优势:
- Louvain 方法高效、适用于大规模网络;
- 谱聚类方法理论清晰、便于可解释;
- 概率模型适合推断复杂多层网络。
三、MATLAB 实现:Louvain 社团检测
在 MATLAB 中,我们通常先构建网络(或载入上一节课程保存的邻接矩阵),然后执行社团检测。
最常见的是 Louvain 算法,它通过模块度 (Q) 的优化自动识别社团。
关键示例:
1 | G = graph(A); |
得到的结果中:
community表示每个节点所属社团编号;Q为模块度值,衡量社团划分质量。
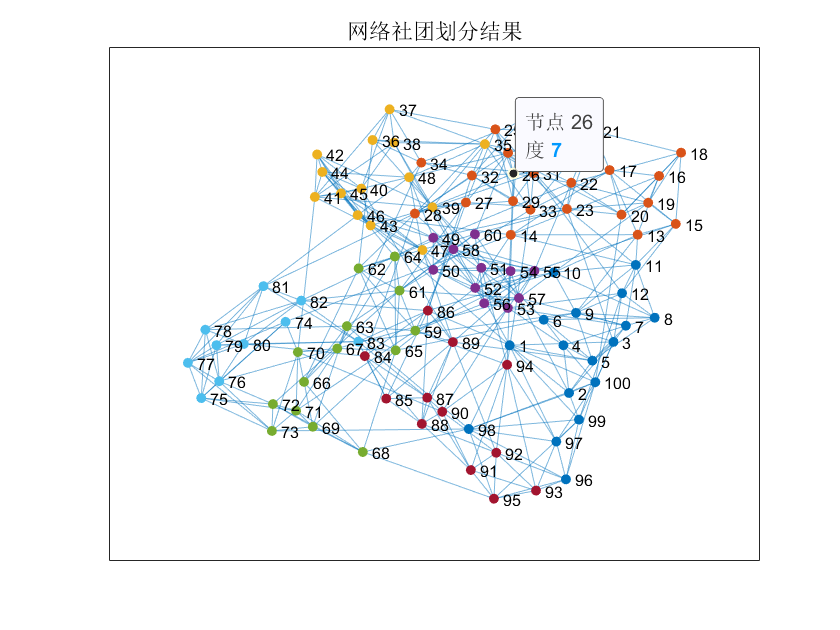
随后可使用 force-directed 布局进行可视化:
1 | p = plot(G, 'Layout', 'force'); |
若模块度 (Q > 0.3),说明网络具有明显的社团结构。
四、模块度与网络类型的关系
模块度 ( Q ) 的定义为:
$$Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j)$$
其中:
- $(A_{ij})$:邻接矩阵;
- $(k_i)$:节点 $(i)$ 的度;
- $(m)$:边总数;
- $(\delta(c_i, c_j))$:若节点 $(i,j) $属于同一社团则为 1,否则为 0。
根据经验:
- (Q > 0.3):网络具有显著社团结构;
- (Q < 0.1):社团结构不明显。
结合前几篇结果,我们可以对网络类型进行对比:
| 网络类型 | 主要特征 |
|---|---|
| 小世界网络 | 高聚类系数 + 短平均路径 |
| 无标度网络 | 度分布呈幂律 |
| 社团网络 | 模块度 (Q) 高,结构分层明显 |
这三类特性经常同时出现在现实系统中,例如社交网络既呈幂律分布,又具有小世界和社团特性。
五、社团结构的功能与桥节点分析
完成社团划分后,我们往往还需识别社团间的关键节点。
这些节点在不同社团间起“桥梁作用”,对信息传播或控制极为关键。
在 MATLAB 中,可以使用介数中心性(Betweenness Centrality)来识别桥节点:
1 | bet = centrality(G, 'betweenness'); |
随后进行可视化:
1 | highlight(p, idx, 'NodeColor', 'k', 'Marker', 's', 'MarkerSize', 8); |
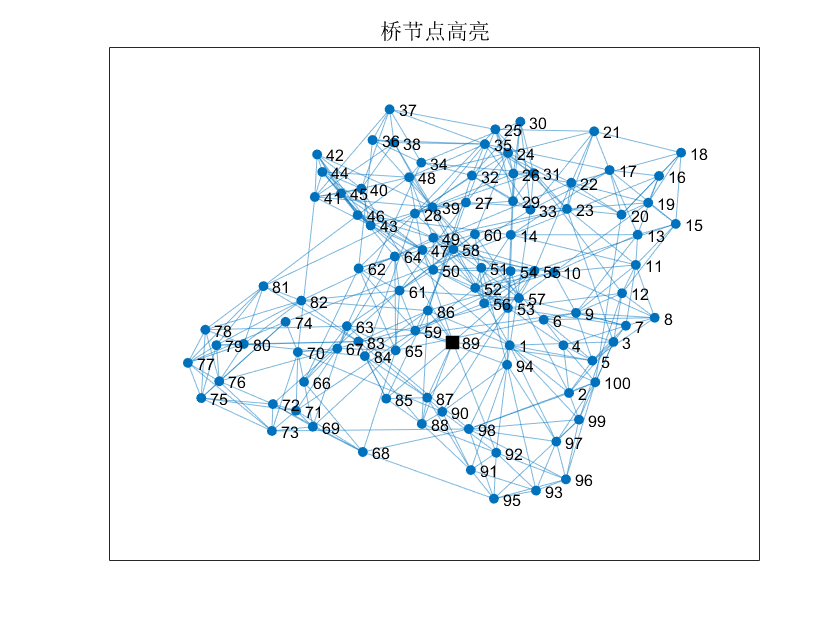
此外,还可以分析不同社团间的连接强度:
1 | imagesc(commMatrix); |
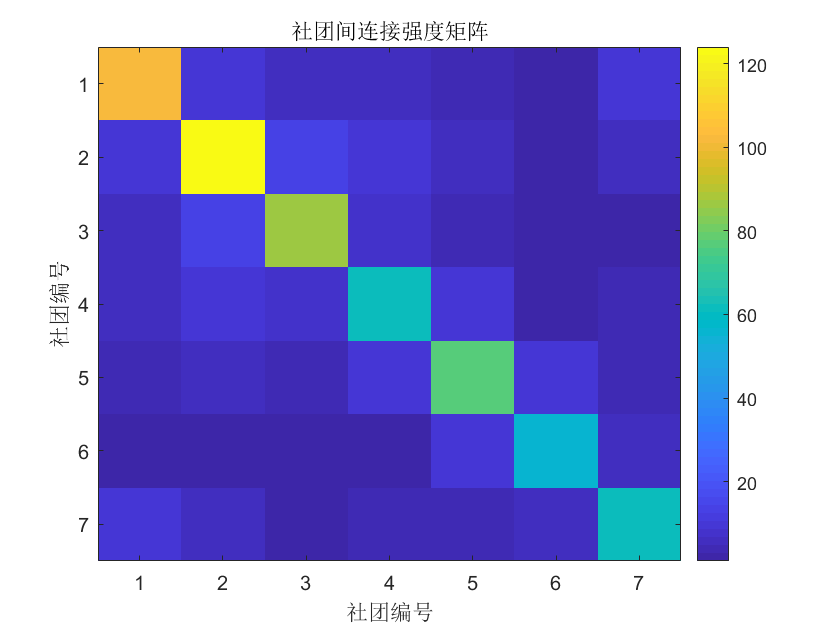
从矩阵图中,我们能清晰看到哪些社团之间的交互更频繁。
六、科研视角的延伸与应用
社团检测不仅是可视化的结果,更是理解复杂系统组织规律的关键工具。
在科研与工程应用中,常见的拓展方向包括:
社团动态演化
研究社团随时间变化的形成与合并过程,例如社交话题的生命周期。多层网络社团检测
当网络存在多种关系(如“合作”与“引用”),需要分析不同层的社团重叠与耦合。基于社团的功能预测
通过节点所属社团,预测其潜在属性或未来连接。
推荐阅读:
- Newman, M. E. J. Networks: An Introduction. Oxford University Press, 2010.
- Fortunato, S. Community Detection in Graphs. Physics Reports, 2010.
七、小结与下一步
本节我们完成了:
- ✅ 理解社团结构的概念与意义;
- ✅ 掌握 Louvain 算法的基本实现;
- ✅ 通过模块度分析网络结构特性;
- ✅ 识别关键桥节点并可视化社团分布。
最后:给大家推荐一个在线复杂计算平台, 欢迎大家进行体验
👉 复杂网络分析平台
支持:
- AI 智能报告生成
- 上传邻接矩阵文件;
- 自动构建网络, 指标一键计算与可视化;
- 网络鲁棒性分析(节点/边攻击)
- 级联失效模型分析
复杂网络仿真入门到精通3: 网络可视化与指标仿真分析
本文为“复杂网络仿真入门到精通”系列的第三篇,前一篇我们学习了如何构建网络(包括随机网络、小世界网络与无标度网络),本篇将聚焦于网络的可视化与基础统计分析,并进一步探讨如何判断一个网络是否具有“小世界”或“无标度”特性。
一、引言
网络不仅仅是由节点与边组成的抽象结构,其拓扑特征往往蕴含了系统行为的重要信息。
从社交网络到神经网络,从交通系统到蛋白质相互作用网络,理解网络的统计特性是揭示系统规律的第一步。
本文将以 MATLAB 为主要工具,介绍:
- 网络可视化方法;
- 网络基本指标计算;
- 小世界与无标度性质的定量分析;
- 幂律分布拟合与验证。
github代码地址:复杂网络学习合集-step3
如访问不了可从下列地址保存:第一个文件夹 下面的 Step3
网盘地址
二、准备数据
可以使用前一篇中的随机、小世界、无标度模型,或导入真实网络。
例如,若已有边列表文件 edge_list.csv:
1 | if isfile('edge_list.csv') |
为了更直观地展示结构特征,可以根据节点度调整节点大小或颜色:
1 | deg = degree(G); |
同理 Python R语言,都可以实现类似的可视化方案
四、网络基本统计指标
1. 节点与边
1 | numNodes = numnodes(G); |
2. 平均度与度分布
1 | deg = degree(G); |
3. 聚类系数与平均最短路径长度
1 | C = mean(clusteringCoefficient(G)); |
clusteringCoefficient(G)可用自定义函数或基于邻接矩阵计算:
2
3
4
5
6
7
8
9
10
11
12
A = adjacency(G);
n = size(A,1);
C = zeros(n,1);
for i=1:n
ki = sum(A(i,:));
if ki > 1
subA = A(i,:) * A * A(:,i);
C(i) = subA / (ki*(ki-1));
end
end
end
五、小世界特性分析
小世界网络一般具有:
- 高聚类系数;
- 短平均路径长度。
为了验证网络是否具有小世界特征,我们需要把网络与同规模、同平均度的随机网络进行对比:
1 | N = numnodes(G); |
六、无标度特性与幂律度分布
无标度网络的节点度分布通常服从幂律形式:
$$P(k) \sim k^{-\gamma}$$
在对数坐标下呈线性关系。
1 | deg = degree(G); |
幂律拟合与参数估计
1 | validIdx = deg > 0; |
若无 plfit 函数,可自行实现或使用简化线性拟合:
1 | logk = log(bins_center(bins_center>0)); |
七、综合分析
| 特性 | 判断依据 | 结论示例 |
|---|---|---|
| 小世界 | ( SWI > 1 ) | 是 |
| 无标度 | 度分布符合幂律 | 是(γ ≈ 2.5) |
若网络同时满足以上两点,则说明其拓扑结构兼具局部聚集与全局稀疏的复杂性特征。
八、结论
本文从可视化入手,系统介绍了复杂网络的基础统计分析方法。
通过对聚类系数、路径长度、度分布及幂律拟合的分析,我们能够初步判断网络类型:
- 小世界网络 → 局部紧密、全局高效;
- 无标度网络 → 度分布长尾,存在“枢纽节点”;
这些特性不仅是理论研究的核心,也为后续的鲁棒性分析与传播动力学仿真提供了基础。
九、下一篇预告
下一篇《复杂网络系列④:网络鲁棒性分析》
我们将深入探讨:
- 网络在随机失效与攻击下的稳定性;
- 节点介数、节点度、中心性等多种重要性指标。
敬请期待。
最后
我们开发了一个在线复杂网络计算平台:
👉 复杂网络分析平台
支持:
- 上传邻接矩阵文件;
- 自动构建网络;
- 指标一键计算与可视化;
- AI 智能报告生成。
复杂网络仿真入门到精通2: 构建网络(邻接矩阵)
系列文章:
- 系列合集
- 下一篇预告:网络可视化与基础统计分析
💡 引言
在复杂网络研究中,“网络构建” 是一切分析与建模的起点。
无论你要研究传播、鲁棒性还是社团结构,第一步都必须拥有一个可计算、可分析的网络结构。而且后续我们的研究,也是研究这个目标网络的特性。
本文以Matlab代码为实例,进行代码说明。
- GitHub 开源代码库:complex-network-study
- 如果上面链接访问不了,可以 网盘提取
从研究角度看,网络的构建主要分为两类:
① 模拟网络(Synthetic Network) —— 基于模型算法生成;
② 实体网络(Empirical Network) —— 来自现实数据的网络。
两类方式各有侧重:
- 模拟网络用于理论研究与算法验证;
- 实体网络用于真实系统建模与特性分析。
而无论哪种方式,最终的核心数据结构都是:邻接矩阵(Adjacency Matrix),邻接表也是可以的。
🧩 一、邻接矩阵的基本形式
假设我们有 ( N ) 个节点,网络可以用一个 ( N \times N ) 的矩阵 ( A ) 表示:
$$
A_{ij} =
\begin{cases}
1, & \text{节点 } i \text{ 与 } j \text{ 有边相连} \
0, & \text{节点 } i \text{ 与 } j \text{ 无连接}
\end{cases}
$$
- 对于无向网络:矩阵对称$A_{ij} = A_{ji}$;
- 对于有向网络:矩阵一般不对称;
- 对于加权网络:$A_{ij}$ 可取任意实数权重。
表达矩阵和后续计算 一般有两种方式:
- 使用二维矩阵(
double或sparse)来存储邻接矩阵,并以矩阵形式进行后续计算。 - 使用邻接矩阵或者邻接表构建图对象(G),并使用这个对象进行后续计算。
🧠 二、构建网络的两条主线
(一)模拟网络(Synthetic Networks)
模拟网络通过算法或数学模型生成人工网络,用于验证理论或测试算法表现。
常见模型包括:
| 网络类型 | 特点 | MATLAB 构建方式 |
|---|---|---|
| 随机网络(Erdős–Rényi, ER) | 边以固定概率 p 随机生成 | sprand(N, N, p) |
| 小世界网络(Watts–Strogatz, WS) | 高聚类 + 短路径 | wattsStrogatz(N, K, p) |
| 无标度网络(Barabási–Albert, BA) | 幂律度分布,存在 Hub 节点 | pref 或自编生长算法 |
✅ 示例:随机网络(ER)模型
1 | N = 10; % 节点数 |
✅ 示例:无标度网络(BA)模型
1 | N = 20; m = 2; |
这些网络模型是复杂网络研究的基础模型,可用于:
- 验证算法;
- 分析理论特性;
- 模拟不同网络拓扑下的行为。
(二)实体网络(Empirical Networks)
实体网络来源于真实世界的数据,是复杂系统的映射结果。
常见来源包括:
| 领域 | 示例 | 数据格式 |
|---|---|---|
| 社会网络 | 微信、微博、协作网络 | .csv, .edge, .gml |
| 生物网络 | 蛋白质相互作用网络 | .graphml, .mat |
| 技术网络 | 电网、交通网络、互联网 | .txt, .json |
| 科研网络 | 引文、合作、知识图谱 | .csv, .gml |
✅ 示例:从边列表构建实体网络
假设你有一个 edges.csv 文件:
| Source | Target |
|---|---|
| 1 | 2 |
| 1 | 3 |
| 2 | 4 |
| 3 | 4 |
MATLAB 构建代码:
1 | data = readtable('edges.csv'); |
✅ 示例:从 .gml 文件导入网络
1 | G = importgraph('network.gml'); % MATLAB R2023a 起支持 |
✅ 示例:从实验或观测矩阵直接读取
1 | A = load('brain_connectivity.mat'); % 神经连接矩阵 |
🔍 三、邻接矩阵的验证与操作
当你成功构建网络后,建议进行基本验证:
1 | N = size(A,1); |
如果矩阵非常稀疏(多数为 0),可转换为稀疏存储:
1 | A = sparse(A); |
🧭 四、延伸阅读:网络构建策略对分析结果的影响
不同的构建方式会显著影响分析结论:
- 模拟网络适合研究拓扑理论与算法鲁棒性;
- 实体网络则能反映真实系统特征与动力学规律。
研究者常在模拟网络上测试方法性能,再在实体网络上验证泛化能力。
⚙️ 五、在线构建与分析平台
我们在平台中提供了一个简易入口:
👉 复杂网络分析平台 - 构建与计算
支持:
- 上传边表 / 邻接矩阵文件;
- 自动构建网络;
- 指标一键计算与可视化;
- AI 智能报告生成。
📘 总结
构建网络是复杂网络研究的起点。
从 模拟网络 到 实体网络,你可以:
- 用 MATLAB 生成理想拓扑结构;
- 从真实数据中提取结构信息;
- 最终得到可分析、可以可视化的邻接矩阵。
下一篇预告:
- 复杂网络入门到精通(三)—— 网络可视化与基础统计
- 我们将使用 MATLAB 展示网络图形化与分布特征。
复杂网络仿真从入门到精通1:关键网络指标解析
引言
复杂网络作为描绘与分析现实世界复杂系统的有力工具,已渗透到自然科学与社会科学的众多领域。从生物网络、技术网络到社会网络,其普适性源于将系统实体抽象为“节点”(Nodes)、将实体间关系抽象为“边”(Edges)的强大能力。对网络拓扑结构的量化分析是理解系统行为、功能与演化规律的基础。
本文旨在系统性介绍复杂网络分析中的核心度量指标,并辅以相应的数学定义,为复杂网络研究扫清障碍。
1. 网络的基本拓扑属性
网络的基本属性是宏观上刻画其规模与连接紧密度的基础。
- 节点数 (Node Count, N) :网络中节点的总数。
- 边数 (Edge Count, M) :网络中边的总数。
- 网络密度 (Density, D) :衡量网络中节点间连接的完备程度。对于一个无向无权网络,其定义为实际存在的边数与可能的最大边数之比。
$$D = \frac{2M}{N(N-1)}$$
密度值介于 0 和 1 之间。$D \to 1$ 表示网络趋近于一个完全图(Clique),节点间连接非常紧密;而 $D \to 0$ 则表示网络是一个稀疏网络。
2. 路径、距离与网络效率
路径相关指标主要用于衡量网络中信息或物质的传输效率与可达性。
平均路径长度 (Average Path Length, L) :网络中所有节点对之间最短路径长度的算术平均值。它反映了网络的全局传输效率。
$$L = \frac{1}{N(N-1)} \sum_{i \neq j} d(i, j)$$
其中,$d(i, j)$ 是节点 $i$ 和 $j$ 之间的最短路径距离。较小的 $L$ 值通常意味着更高的网络通信效率。网络直径 (Diameter, D_max) :网络中所有节点对之间最短路径长度的最大值。它定义了网络中信息传输所需的最长时延。
3. 聚类效应与社区结构
这些指标用于量化网络中的局部聚集程度和中尺度结构。
平均聚类系数 (Average Clustering Coefficient, C) :衡量网络中节点“抱团”或形成紧密邻域的平均趋势。一个节点 $i$ 的局部聚类系数 $C_i$ 定义为其邻居节点之间实际存在的边数与可能的最大边数之比。
$$C_i = \frac{2E_i}{k_i(k_i-1)} $$
其中,$k_i$是节点$i$的度(邻居数),$E_i$是其
$k_i$个邻居之间实际存在的边数。网络的平均聚类系数即为所有节点$C_i$的平均值:
$$C = \frac{1}{N} \sum_{i=1}^{N} C_i$$社区 (Community) :指网络中由一些连接紧密的节点组成的子图,这些子图内部的连接密度远高于其与网络其余部分的连接密度。
模块度 (Modularity, Q) :衡量网络社区结构划分质量的常用指标。其核心思想是比较社区内部实际存在的边数与在相同节点度和社区划分下的随机期望边数。
$$Q = \frac{1}{2M} \sum_{i,j} \left[ A_{ij} - \frac{k_i k_j}{2M} \right] \delta(c_i, c_j)$$
其中,$A_{ij}$ 是邻接矩阵元素,$k_i$ 是节点 $i$ 的度,$\delta(c_i, c_j)$ 函数当节点 $i, j$ 属于同一社区时为 1,否则为 0。$Q$ 值越高(通常认为大于 0.3),表明社区划分越显著。
4. 节点中心性度量
中心性指标用于识别网络中最重要的节点,但“重要性”的定义因场景而异。
度中心性 (Degree Centrality) :最直接的中心性度量,定义为节点的连接数(度)。对于有向图,分为入度和出度。标准化的度中心性为:
$$C_D(i) = \frac{k_i}{N-1}$$介数中心性 (Betweenness Centrality) :衡量一个节点作为网络中其他节点对之间最短路径“桥梁”的程度。
$$C_B(v) = \sum_{s \neq v \neq t}
\frac{\sigma_{st}(v)}{\sigma_{st}}$$其中,$\sigma_{st}$ 是从节点$s$到$t$
的最短路径总数,$$\sigma_{st}(v)$$
是这些路径中经过节点 $v$的数量。高介数的节点是网络信息流的关键瓶颈。接近度中心性 (Closeness Centrality) :衡量一个节点到网络中所有其他节点的平均距离的倒数。它反映了节点作为信息传播中心的能力。
$$C_C(v) = \frac{N-1}{\sum_{t \neq v} d(v, t)}$$PageRank :一种衡量节点递归重要性的算法。一个节点的 PageRank 值不仅取决于指向它的链接数量,还取决于这些链接来源节点的重要性。
5. 常见网络拓扑模型
- 无标度网络 (Scale-Free Network) :许多真实网络的度分布服从幂律分布(Power-law distribution),即 $$P(k) \sim k^{-\gamma}$$,其中 $P(k)$是度为 $k$ 的节点比例,$gamma$ 是幂律指数。这类网络具有少量度极高的“中心节点”(Hubs)和大量度很低的“末梢节点”,呈现“贫富分化”现象。无标度网络对随机故障具有鲁棒性,但对针对中心节点的蓄意攻击则表现出脆弱性。
- 小世界网络 (Small-World Network) :这类网络同时具有高聚类系数(类似规则网络)和短平均路径长度(类似随机网络)的特征。该特性由 Watts 和 Strogatz 于 1998 年提出,广泛存在于社会、生物和技术网络中。
实践(Matlab代码版)
对上述指标的精确计算与综合分析,是揭示任何复杂系统内在机制的关键。然而,手动计算和分析过程繁琐且易错。
matlab 实现代码请访问:
https://github.com/XuXING0430/complex-network-study
为了促进学术研究与应用探索,我们开发了一个计算平台,该平台旨在提供一个高效、精准且用户友好的网络分析解决方案。可以直接进行体验:
还包括以下的功能:
- 便捷的数据导入 :支持多种标准网络数据格式。
- 自动化的指标计算 :一键生成包括本文所述在内的数十种关键网络指标。
- 深度 AI 分析报告 :结合计算结果,提供对网络结构与特性的智能化解读。
- 图表可视化 :相关指标出图表
